动态查找树

动态查找树主要有：二叉查找树（Binary Search Tree），平衡二叉查找树（Balanced Binary Search Tree），红黑树(Red-Black Tree )，B-tree/B+-tree/ B*-tree (B~Tree)平衡多路查找树

B-tree

B 树是为了磁盘或其它存储设备而设计的一种多叉平衡查找树。与红黑树类似，但在降低磁盘I/0操作方面要更好一些。许多数据库系统都一般使用B树或者B树的各种变形结构。B树与红黑树最大的不同在于，B树的结点可以有许多子女，从几个到几千个。不过B树与红黑树一样，一棵含n个结点的B树的高度也为O(lgn)，但可能比一棵红黑树的高度小许多，因为它的分支因子比较大。

B-Tree的结构可以如下表示：

1
2
3
4
5
6
7
8
9
10
typedef struct {
    /*文件数*/
    int  file_num;
    /*文件名(key)*/
    char * file_name[max_file_num];
    /*指向子节点的指针*/
     BTNode * BTptr[max_file_num+1];
     /*文件在硬盘中的存储位置*/
     FILE_HARD_ADDR offset[max_file_num];
}BTNode;

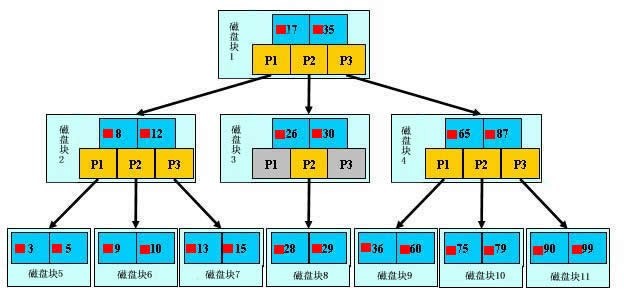
比如利用上图模拟查找文件29的过程：

  1. 根据根结点指针找到文件目录的根磁盘块1，将其中的信息导入内存。【磁盘IO操作 1次】
  2. 此时内存中有两个文件名17、35和三个存储其他磁盘页面地址的数据。根据算法我们发现：17<29<35，因此我们找到指针p2。
  3. 根据p2指针，我们定位到磁盘块3，并将其中的信息导入内存。【磁盘IO操作 2次】
  4. 此时内存中有两个文件名26，30和三个存储其他磁盘页面地址的数据。根据算法我们发现：26<29<30，因此我们找到指针p2。
  5. 根据p2指针，我们定位到磁盘块8，并将其中的信息导入内存。【磁盘IO操作 3次】
  6. 此时内存中有两个文件名28，29。根据算法我们查找到文件名29，并定位了该文件内存的磁盘地址。

分析上面的过程，发现需要3次磁盘IO操作和3次内存查找操作。关于内存中的文件名查找，由于是一个有序表结构，可以利用折半查找提高效率。至于IO操作是影响整个B树查找效率的决定因素。

B树的插入：主要的是一个分裂操作

B树的删除：情况比较多，略

B+-tree

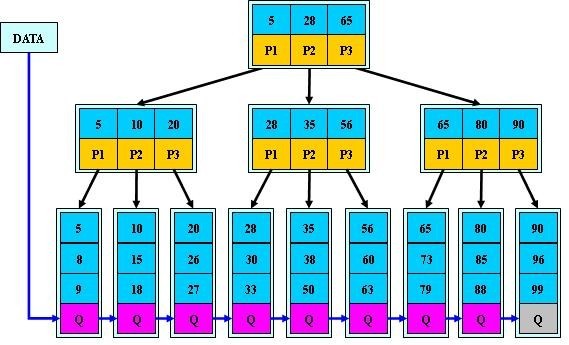
为什么说B+-tree比B 树更适合实际应用中操作系统的文件索引和数据库索引？

  1. B+-tree的磁盘读写代价更低，B+-tree的非叶子节点并没有指向关键字具体信息的指针。因此其非叶子节点相对B 树更小，盘块所能容纳的关键字数量更多，一次性读入内存中的需要查找的关键字也就越多
  2. B+-tree的查询效率更加稳定，只有叶子节点存放了指向关键字具体信息的指针，每一次查找都需要从根节点走到叶子节点
  3. B+-tree有指向兄弟节点的指针，对于范围查找非常方便

B*-tree

B*-tree是B+-tree的变体，在B+树的基础上(所有的叶子结点中包含了全部关键字的信息，及指向含有这些关键字记录的指针)，B树中非根和非叶子结点再增加指向兄弟的指针；B树定义了非叶子结点关键字个数至少为(2/3)*M，即块的最低使用率为2/3（代替B+树的1/2）

B*树分配新结点的概率比B+树要低，空间使用率更高

红黑树

红黑树，本质上来说就是一棵二叉查找树，但它在二叉查找树的基础上增加了着色和相关的性质使得红黑树相对平衡，从而保证了红黑树的查找、插入、删除的时间复杂度最坏为O(log n)

或者可以说：通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径会比其他路径长出俩倍，因而是接近平衡的。

具有以下5条性质：

  1. 每个结点要么是红的，要么是黑的。
  2. 根结点是黑的。
  3. 每个叶结点（叶结点即指树尾端NIL指针或NULL结点）是黑的。
  4. 如果一个结点是红的，那么它的俩个儿子都是黑的。
  5. 对于任一结点而言，其到叶结点树尾端NIL指针的每一条路径都包含相同数目的黑结点。

树的左旋：

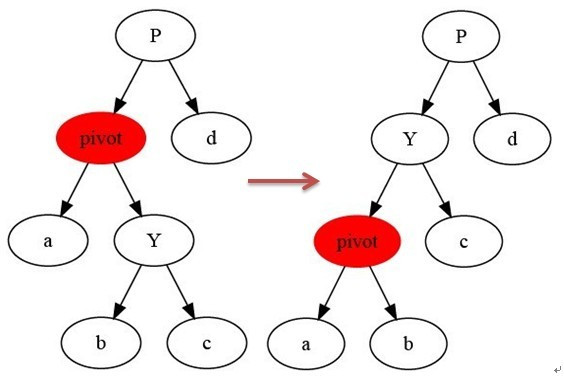
树的右旋：

二叉查找树的插入：

在二叉查找树中查找z待插入的位置，如果插入结点z小于当前遍历到的结点，则到当前结点的左子树中继续查找，如果z大于当前结点，则到当前结点的右子树中继续查找，找到待插入的位置，如果z依然比此刻遍历到的新的当前结点小，则z作为当前结点的左孩子，否则作为当前结点的右孩子。

红黑树的插入相当于在二叉查找树插入的基础上，为了重新恢复平衡，继续做了插入修复操作

插入过程：

  • 如果插入的是根结点，因为原树是空树，此情况只会违反性质2，所以直接把此结点涂为黑色。
  • 如果插入的结点的父结点是黑色，由于此不会违反性质2和性质4，红黑树没有被破坏，所以此时也是什么也不做。
  • 插入修复情况1： 如果当前结点的父结点是红色且祖父结点的另一个子结点（叔叔结点）是红色
    • 对策： 将当前结点的父结点和叔叔结点涂黑，祖父结点涂红，把当前结点指向祖父结点，从新的当前结点重新开始算法
  • 插入修复情况2： 当前结点的父结点是红色,叔叔结点是黑色，当前结点是其父结点的右子
    • 对策： 当前结点的父结点做为新的当前结点，以新当前结点为支点左旋。即如下代码所示：
  • 插入修复情况3： 当前结点的父结点是红色,叔叔结点是黑色，当前结点是其父结点的左子
    • 对策： 父结点变为黑色，祖父结点变为红色，在祖父结点为支点右旋

删除过程：

  • 当前结点是红+黑色
    • 解法，直接把当前结点染成黑色，结束此时红黑树性质全部恢复
  • 当前结点是黑+黑且是根结点
    • 解法：什么都不做，结束
  • 删除修复情况1： 当前结点是黑+黑且兄弟结点为红色(此时父结点和兄弟结点的子结点分为黑)
    • 解法：把父结点染成红色，把兄弟结点染成黑色，之后重新进入算法
  • 删除修复情况2： 当前结点是黑加黑且兄弟是黑色且兄弟结点的两个子结点全为黑色
    • 解法：把当前结点和兄弟结点中抽取一重黑色追加到父结点上，把父结点当成新的当前结点，重新进入算法
  • 删除修复情况3： 当前结点颜色是黑+黑，兄弟结点是黑色，兄弟的左子是红色，右子是黑色
    • 解法：把兄弟结点染红，兄弟左子结点染黑，之后再在兄弟结点为支点解右旋，之后重新进入算法
  • 删除修复情况4： 当前结点颜色是黑-黑色，它的兄弟结点是黑色，但是兄弟结点的右子是红色，兄弟结点左子的颜色任意
    • 解法：把兄弟结点染成当前结点父结点的颜色，把当前结点父结点染成黑色，兄弟结点右子染成黑色，之后以当前结点的父结点为支点进行左旋，此时算法结束

平衡二叉树

平衡二叉查找树，又称 AVL树。 它除了具备二叉查找树的基本特征之外，还具有一个非常重要的特点：它 的左子树和右子树都是平衡二叉树，且左子树和右子树的深度之差的绝对值（平衡因子 ） 不超过1。 也就是说AVL树每个节点的平衡因子只可能是-1、0和1（左子树高度减去右子树高度）。

比如空节点是-1，叶子节点是0，非叶子节点的height往根节点递增，比如在下图中认为树的高度为h=2

有两种调整方法，左旋转和右旋转

平衡二叉树的性能优势：

  • 其查找的时间复杂度为O(logN)

平衡二叉树的缺陷：

  • 动态插入和删除的代价也随之增加，此处比红黑树查
  • 树高高于多路查找树
  • 在大数据的查找环境下二叉查找树不再适用，应该使用多路查找树