常见的排序算法
文章目录
常见的排序算法
冒泡排序、插入排序、选择排序、希尔排序、堆排序、归并排序、快速排序
冒泡排序: 平均时间复杂度O(n^2),最好情况复杂度O(n)
步骤:
- 比较相邻的元素。如果第一个比第二个大,就交换他们两个。
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
- 针对所有的元素重复以上的步骤,除了最后一个。
- 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
插入排序: 时间复杂度:O(n^2),最优时间复杂度:O(n)
步骤:
- 从第一个元素开始,该元素可以认为已经被排序
- 取出下一个元素,在已经排序的元素序列中从后向前扫描
- 如果该元素(已排序)大于新元素,将该元素移到下一位置
- 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置
- 将新元素插入到该位置后
- 重复步骤2~5
选择排序: 时间复杂度:O(n^2),最优时间复杂度:O(n^2)
步骤:
首先在未排序序列中找到最小元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小元素,然后放到已排序序列的末尾。
希尔排序: 时间复杂度:根据步长而不同,最优时间复杂度:O(n)
步骤:
对数组进行分区,按照步长进行分区
对每个分区应用插入排序
再把步长缩减成1/2,再应用插入排序:
直到步长为一
堆排序: 时间复杂度:O(nlogn),最优时间复杂度:O(nlogn)
说明:
堆(二叉堆)可以视为一棵完全的二叉树
二叉堆一般分为两种:最大堆和最小堆
最大堆:
- 最大堆中的最大元素值出现在根结点(堆顶)
- 堆中每个父节点的元素值都大于等于其孩子结点(如果存在)
最小堆:
- 最小堆中的最小元素值出现在根结点(堆顶)
- 堆中每个父节点的元素值都小于等于其孩子结点(如果存在)
步骤:
先建立一个堆(最小或最大都可以)

映射方式按照如下的公式进行:
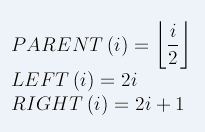
然后进行堆调整,比如下图是按照最大堆的方式进行调整中的一趟:
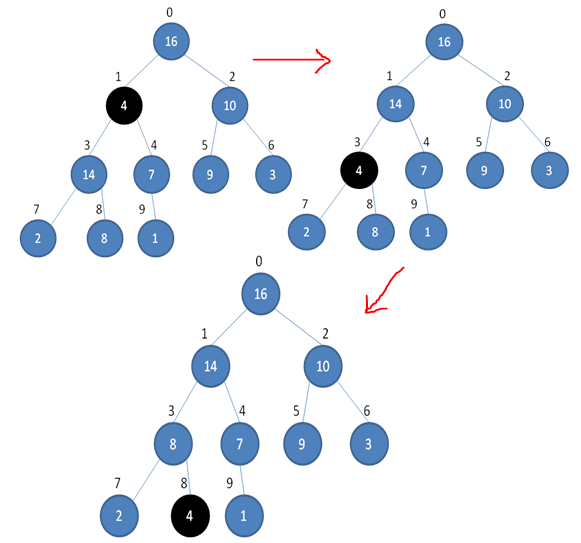
取出堆顶元素,在重复进行以上步骤,直到只剩一个元素

归并排序: 时间复杂度:O(nlogn),最优时间复杂度:O(n)
步骤:归并操作(merge),也叫归并算法,指的是将两个已经排序的序列合并成一个序列的操作。归并排序算法依赖归并操作。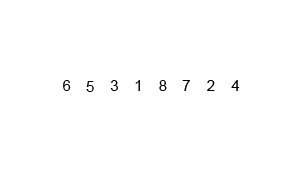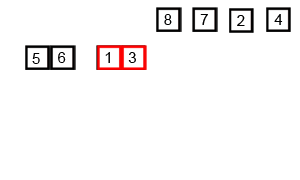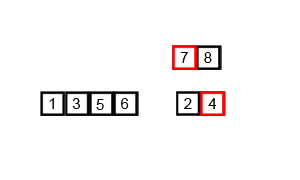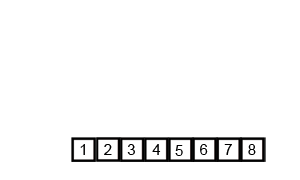
快速排序: 时间复杂度:O(nlogn),最优时间复杂度:O(nlogn)
步骤:
- 从数列中挑出一个元素,称为”基准”(pivot),
- 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区结束之后,该基准就处于数列的中间位置。这个称为分区(partition)操作。
- 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。