四元数与欧拉角
1.欧拉角(eulerianAngle)
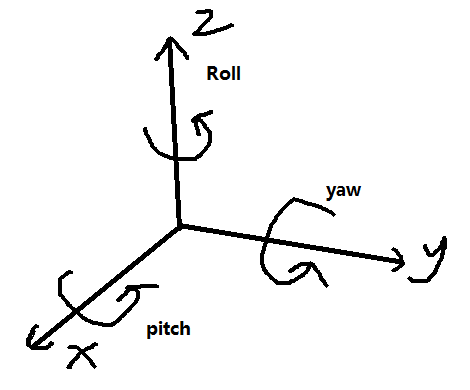
欧拉角用最简单的α,ψ,φ分别表示绕世界坐标系下x,y,z轴的旋转角度,绕x,y,z轴旋转的角度分别叫做pitch(俯仰角),yaw(偏航角),roll(翻滚角)
2.四元数(quaternion)
- 定义
四元数使用了一个三维向量表示转轴和一个角度表示绕此旋转轴的旋转角度讲,即(x,y,z,w)
w=cos(θ/2)
x=ax*sin(θ/2)
y=ay*sin(θ/2)
z=az*sin(θ/2)
其中ax,ay,az表示轴的矢量,θ为绕轴旋转角度
相关计算
q=w+xi+yj+zk
求模:|q|^2=w^2+x^2+y^2+z^2
共轭:q=w-xi-yj-z*k
求逆:q^-1=q*/|q|
用四元数旋转矢量
给定一个矢量V,再给定一个旋转四元数q,让v按q旋转
v=(x,y,z,0)
v’=qvq^-1
四元数插值slerp(spherical linear interpolation)
slerp(q0,q1,t)=q0*sin((1-t)θ)/sinθ+q1*sin(tθ)/sinθ
其中θ=arcos(q0·q1)
3.四元数与欧拉角的转化
欧拉角转换为四元数:

四元数转化为欧拉角:
Tip:atan2(a,b)取值范围介于(-π,+π],表示点(b,a)与X轴的夹角
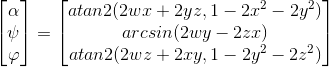
more information about quaternion refered to Understanding Quaternions